2020-05-14 16:38:30 辽宁华图公考问答 http://ln.huatu.com/wenda/ 文章来源：辽宁华图
方程法作为数量关系中的万能方法，也是各位考生最熟悉的方法。方程法在我们贯穿我们整个义务教育，也是大家遇到数量关系第一个想到的方法，但关于方程法，各位真的熟悉或者能灵活应用吗?
首先我们要明确一点，方程法使用的范围是条件中存在明显等量关系的题型，譬如和差倍比、浓度问题、利润问题、行程问题、工程问题、牛吃草问题等等。
我们都知道方程法分为三步：设、列、解。在这里给大家强调一下，方程法最关键的一步就是如何巧设未知数，一般是问什么设什么，当然个别题型设中间量也是方便计算的。列的话就根据条件中的等量关系进行列式。传统解方程的方法是合并同类项，系数化为1，但是在我们数量关系中我们可以采取代入法进行寻求答案，可以加快我们的做题速度。当然还有一些不定方程的习题，和我们等式方程也是异曲同工之效。接下来我们通过例题来强化一下。
例题一：小明负责将某农场的鸡蛋运送到小卖部。按照规定，每送达1枚完整无损的鸡蛋，可得运费0.1元;若有鸡蛋破损，不仅得不到该枚鸡蛋的运费，每破损一枚鸡蛋还要赔偿0.4元。小明10月份共运送鸡蛋25000枚，获得运费2480元。那么，在运送过程中，鸡蛋破损了：A. 20枚 B. 30枚 C. 40枚 D. 50枚
解析：设破损枚数为x，可得(25000-x)×0.1-0.4x=2480，解得x=40。因此，选择C选项。
解法二：
第二步，假设25000枚鸡蛋全部完好无损，总共得到的运费为25000×0.1=2500(元)，每破损一枚鸡蛋，不仅得不到该鸡蛋的运费0.1元，还要赔偿0.4元，共损失0.5元。则破损枚数为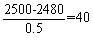
(枚)。因此，选择C选项。
例题二：小张家养了一只大狗和一只小狗。现在，小狗的体重只有大狗的一半。如果两只狗的体重各增加5千克，那么小狗的体重将达到大狗的60%。据此可知，若两只狗的体重各增加10千克，小狗、大狗的体重比将会是：
A.1∶2 B.2∶3 C.3∶4 D.4∶5
解析：本题考虑设置中间量，设小狗的重量为x，则大狗的重量为2x，则由题意，x+5=(2x+5)×60%，解方程得x=10，可知小狗重10千克，大狗重20千克。若各增加10千克，则体重比为(10+10)∶(20+10)=2∶3。因此，选择B选项。
例题三：某次田径运动会中，选手参加各单项比赛计入所在团体总分的规则为：一等奖得9分，二等奖得5分，三等奖得2分。甲队共有10位选手参赛，均获奖。现知甲队最后总分为61分，问该队最多有几位选手获得一等奖?
A. 3 B. 4 C .5 D. 6
解析：设获得一等奖的有x位选手、获得二等奖的有y位选手、获得三等奖的有z位选手。根据共10位选手参赛和总分为61分，可列不定方程组：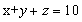
①，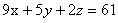
②，②-①×5可得：
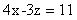。问该队最多有几位选手获得一等奖，最值代入，优先代入D选项，x=6，z无整数解，排除;代入C选项，若x=5，z=3，y=2，满足题意。因此，选择C选项。
希望给大家带来一些帮助，至少大家的数量关系还是可以试着抢救一下的，留道例题给大家练练手。
练习一：小张需租某店铺制作贩售绿茶。他计划以8万元现金及若干固定袋数的绿茶作为一年租金。若每袋茶叶售价75元，则一年租金等价于每平方米70元;若每袋茶叶在原价的基础上再涨价三分之一，则一年租金相当于每平方米80元。那么该店铺的面积为多少平方米?
A .1600 B. 2000 C .2500 D. 3000
练习二：某旅游公司有能载4名乘客的轿车和能载7名乘客的面包车若干辆，某日该公司将所有车辆分成车辆数相等的两个车队运送两支旅行团。已知两支旅行团共有79人，且每支车队都满载，问该公司轿车数量比面包车多多少辆?A. 5 B. 6 C. 7 D. 8
（编辑：辽宁华图07）
贴心微信客服
贴心QQ客服
